300 Mesurer une distance ou une hauteur sans rien…
300 Mesurer une distance ou une hauteur sans rien…
Pour ce faire on va utiliser une astuce de visée, en fait, une règle de base très ancienne, appelée règle des millièmes. Cette mesure est connue depuis fort longtemps et ne nécessite de posséder aucun appareil particulier. Il faudra cependant avoir une idée précise d'un certain nombre de rapport de grandeurs, grandeurs dont on dispose toujours sur soi, bien évidement... A savoir nos doigts, nos mains, nos bras, c-à-d nos propres dimensions corporelles... C'est d'ailleurs ainsi que nos anciens définissaient les mesures avec un pouce, un empan, une coudée, un pas, une brassée (ou toise), une lieue**, etc... Toutes ces grandeurs découlaient d'éléments visuels (physiologiques en premier), de leur environnement pratique. Bien.
*mesures anciennes : Voir - Trucs & Astuces1 - 097 Astuces de mesures en tout genre...
** lieue : à l'origine, la lieue était la distance de l'horizon vue en mer par un marin, au niveau de l'eau en se tenant debout dans une barque. Cela représente environs un peu plus de 2 miles nautiques (Nm) soit environs 4 kms. A terre, c'était aussi la distance que pouvait parcourir un homme en marchant normalement durant 1 heure, soit à peu près, également 4 kms (donc en pratique, même valeur).
La règle du millième...
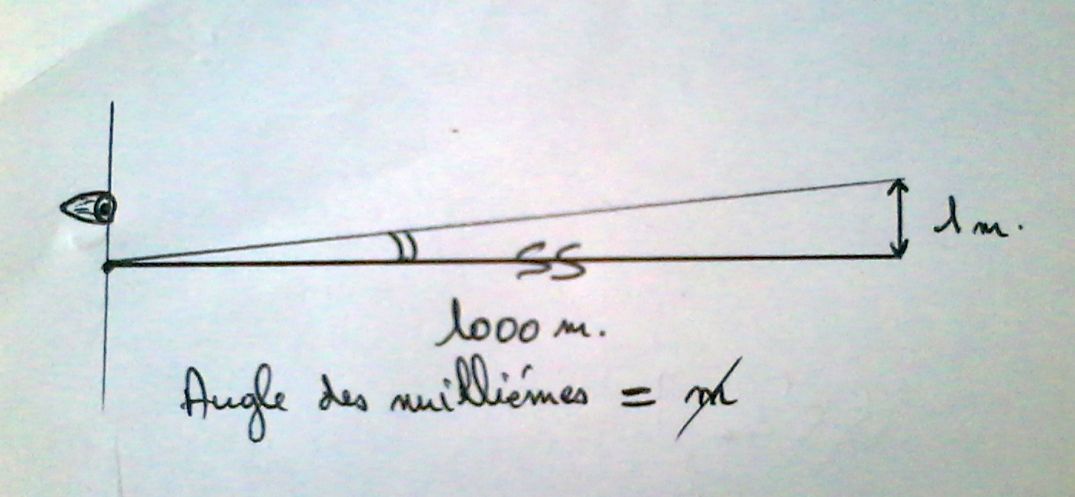
Par définition, le "millième" (s'écrie "m barré" : ₥) est l'angle sous lequel on voit un objet de 1 mètre de hauteur à 1000 m de distance en le regardant à l'horizontal devant soi. Cet angle en pratique est donc très petit.
Rappel des rapports et expressions de mesures utilisées pour les angles...
Un angle peut se mesurer en degrés, grades ou millièmes et on va trouver :
Un cercle = 360° = 400 gr = 3600 ₥.
On voit donc que un degré équivaut à 10 millièmes ou encore que un millième vaut 6 minutes de degré (puisqu'il y a 60 minutes par degré d'angle). Il faut commencer par se familiariser avec ces unités afin de pouvoir passer aisément d'un l'une à l'autre.
Reste ensuite à avoir une idée bien précise de nos éléments physiologiques, propres à chacun de nous pour en faire nos références lors de visées pour mesures. Ainsi, il faut connaître l'épaisseur de ses doigts, l'épaisseur de son poing fermé, la longueur de son bras tendu, et de tout un tas d'autres repères que chacun devra mesurer et connaître. Bien sûr, nous prendrons ces dimensions en centimètres nous autres, car désormais nous possédons ce système de mesure précis et il fait partie intégrante de nos repères visuels au quotidien. Pour moi par exemple, je sais que 2 doigts valent 4 centimètres. Mais on pourrait tout aussi bien conserver les unités de nos anciens que cela ne changerait rien !
Pour ma part, si je mesure toutes ces références à connaître cela donne...
Epaisseur des doigts (index, majeur, annulaire) : 2 cm.
Largeur du pouce (à la base sur la matrice de l'ongle) : 25 mm (un inch GB vaut 25,4 mm !).
Epaisseur de la main poing fermé : 10 cm.
Longueur bras tendu, depuis l'oeil jusqu'au poing fermé : 60 cm.
Longueur depuis main, bras tendu, à l'épaule opposée (la brassée) : 1m.
Longueur main à main, bras tendus à l'horizontal : 1,70 cm.
Hauteur depuis le sol, bras levé avec main tendue : 2 m.
Une coudée G/D : 46 cm. Un empan main G : 21 cm. et main D : 20cm.
Voici donc toutes les références que moi (et moi seul) je vais pouvoir disposer pour calculer ensuite toutes sortes de grandeur, hauteur ou distance en utilisant la règle des millièmes.
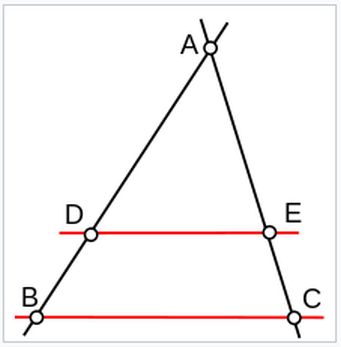
En fait avec ce système, on va utiliser les fameuses "relations dans un triangle" du célèbre théorème de Thalès. (une droite coupant un triangle quelconque parallèlement à l'un de ses côtés donnera les mêmes rapports de dimensions entre les divers segments de tous ses côtés). Connaissant en plus un angle (nombre de degrés ou de millièmes observés), on connaîtra toutes les autres mesures restantes de cette figure.
Voir un exemple sur ce dessin ici...
Si la droite DE coupe le triangle quelconque ABC en étant parallèle à BC, les 2 triangles ADE et ABC sont semblables. Mais en plus les segments de ces triangles seront tous proportionnels et ses angles égaux.
A savoir, AD/AB = AE/AC = DE/BC
Les angles AED et ACB sont identiques.
Les angles ADE et ABC sont identiques.
A partir de tous ces éléments, on pourra donc mesurer un objet en comparant avec nos divers "segments de mesures" et ensuite établir la relation qui permettra de calculer les dimensions exactes à partir de ces rapports.
Qu’on se le dise …et bon vent !
Retour trucs-astuces-3...
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 246 autres membres


