Enigme 180 – La mesure impossible serait-elle la meilleure…

Enigme 180 – La mesure impossible serait-elle la meilleure…

Nous sommes en Belgique dans une grande école d’architecture et un professeur donne un cours de géophysique. Le thème d’aujourd’hui porte sur l’emploi du Stadia et l’utilisation du télémètre, en topographie.

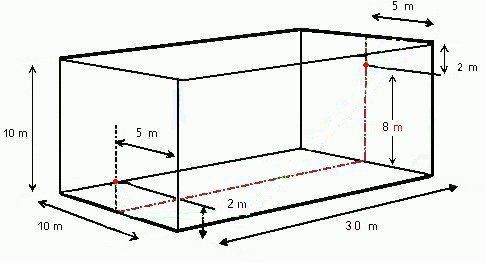
Comme exercice, le professeur propose alors à son groupe d’étudiants de se rendre dans la salle de squash juste à côté, pour un exercice pratique, grandeur nature. Auparavant ce professeur a repéré sur les murs de cette salle deux points distincts. L’un à 2 m du sol au milieu de la largeur du mur d’entrée et l’autre sur le mur opposé du fond, à 2 m du plafond cette fois. Ces deux points spécifiques sont marqués à la peinture (les 2 points rouge, de la figure) sur le milieu donc, de la largeur des deux murs.

C’est alors qu’il leur soumet le problème suivant…

Je ne dispose d’aucun appareil (pas de Stadia ni télémètre) cette fois et je veux quand même mesurer la distance linéaire la plus courte entre ces deux points. Pour cela, il faudra donc suivre les différentes surfaces de la pièce (c’est par exemple pour faire passer une ligne électrique, une fibre optique, n'importe…). Pour cela, vous disposez seulement d’un ruban d’arpenteur gradué jusqu’à 50 m de longueur.

Pouvez vous me dire quelle est la longueur la plus courte (en suivant les plans ou murs de la pièce) entre ces deux points repérés sur les murs, en utilisant uniquement ce ruban d’arpenteur ? Une échelle est à disposition si besoin.

La salle de squash mesure 30 m de long pour 10 m de largeur et aussi 10 m de hauteur. Les points marqués sont donc respectivement, à 2m (mur d’entrée) et 8 m (mur du fond) du sol.

Quelle est donc la distance linéaire la plus courte entre ces deux points rouges ?

Enigme 180.jpg