097 Trucs & Astuces de mesures en tout genre...
097 Trucs & Astuces de mesures en tout genre…
Un mètre improvisé…
Parfois on a besoin de mesurer quelque chose et pas de chance, rien sous la main pour ce faire. Mon père qui était menuisier ébéniste m'a appris bien des trucs que je donne volontiers.
1) L'Empan* est la distance mesurée entre l'extrémité du pouce et le majeur main étendue à plat. Cette distance pour un individu normal est toujours très proche de 20 cm.
Cinq empans consécutifs donneront donc aux environs d'un mètre.
2) La Coudée fait théoriquement 50 cm. C'est la longueur de l'avant bras tendu et doigts allongés. Pour ma part, elle fait, mesurée, 45cm et si j'ajoute avec ma main gauche, 3 doigts serrés, j'arrive juste à 50 cm ! Donc bon repère.
3) La brassée est la distance mesurée entre l'extrémité d'un bras tendu à l'horizontal et l'épaule opposée. On repli le second bras sur cette épaule et on peut ainsi mesurer une corde en la prenant dans la main tendue et en la posant sur l'épaule opposée. Pour ma part cette mesure fait 101, 102 cm environs. Il suffit de le faire plusieurs fois pour connaître sa longueur moyenne mesurée. Vous avez donc ainsi avec vous et toujours, un mètre de référence assez juste.
4) La hauteur bras tendu est souvent proche de 2 m. Pour ma part elle fait exactement 2 mètres. C'est donc une bonne référence pour mesurer principalement des hauteurs cette fois.
NB : si vous avez quelque chose à mesurer que vous ne pouvez pas porter à vos épaules, à votre bras, ou en verticale eh bien vous cherchez un bâton, un bout de ficelle ou autre bout de tissu que vous calibrez à cette référence de mesure.
* Empan : Voir ici une page extraite du CRDP de Montpellier, juste pour le fun. Article très intéressant sur les mesures et règles d'Or des bâtisseurs de cathédrales, ici…
Mesurer une hauteur…
Un jour ou l'autre, il nous arrive d'avoir besoin de connaître la hauteur de son mât au dessus de l'eau, antenne comprise… Personnellement, j'ai eu besoin de mesurer la hauteur totale de mon grand mât, pour la première fois, à Florianopolis au Brésil où 3 ponts successifs paraissaient "limite" pour passer dessous ...Puis encore au Venezuela pour mesurer la hauteur de la ligne électrique en travers du Caroni pour aller visiter le Salto Angel…/…
Les occasions ne manquent pas pour cet exercice…
Alors comment faire pour connaître cette hauteur fatidique qui vous permettra de vous engager sous un danger sans vous donner la frayeur de votre vie ?
En fait il existe plein de méthodes qui permettraient de mesurer cette hauteur, je vais en donner ici quelques unes, les plus faciles à mettre en œuvre.
Première méthode…
La plus simple, en utilisant la fameuse relation de Thalès.
Dans ce rapport remarquable on a le ratio h/H qui est égal au ratio d/D.
d = la distance entre l'oeil et la règle.
D = la distance entre l'oeil et le pied du mât.
h = La hauteur mesurée sur la règle.
H = la hauteur à mesurer, en l' occurrence la hauteur du mât !
Bien sûr, il faut mettre toutes les mesures de manière identique (m, cm ou mm).
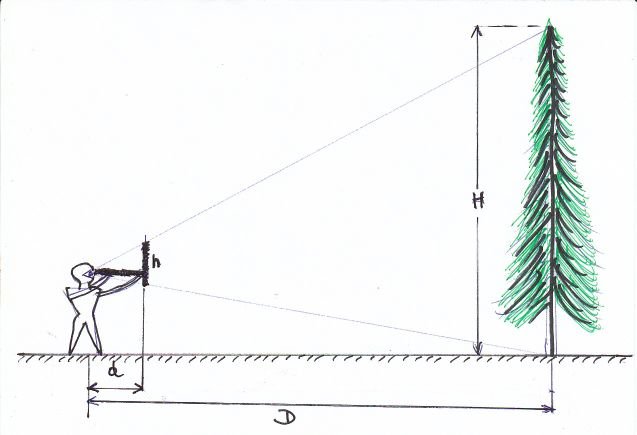
Connaissant h, d, et D on peut calculer aisément H. Dans la formule h/H = d/D on en déduit que H = D/d X h (voir dessin du bûcheron, en dessous - idem).
Pour ce faire il suffit de tenir dans votre main, bras tendu une règle, verticalement. Vous faites coïncider l'extrémité 0 de la règle avec le haut du mât et de l'autre vous déplacez votre pouce jusqu'à faire coïncider le bas du bateau à hauteur de la flottaison, sur la règle. Ne lâchez pas le zéro en haut ni ce repère. Il suffit alors de lire cette longueur mesurée en cm. Vous aurez donc h.
Vous avez la longueur d : la longueur de votre bras allongé jusqu'à la règle (dans mon cas : 56 cm). Vous connaissez D, il suffit de mesurer. Connaissant ces valeurs, vous n'avez plus qu'à utiliser ce rapport de Thalès.
Voici en image comment réaliser cette observation pour faire le calcul avec le rapport de Thalès. On fait coïncider le zéro au sommet du mât puis on monte le pouce jusqu'à à venir en face de la flottaison du bateau.

Seconde méthode, la croix du bûcheron…
Cette fois, il vous faudra deux bâtons de même longueur (entre 20cm et 70 cm suivant la hauteur à mesurer et la distance d'éloignement). Il faut que vous les teniez à bout de bras, perpendiculaire l'un à l'autre. L'un horizontal qui vous touchera le visage sous l'œil et l'autre vertical à toucher le premier comme sur le dessin. Une fois établie cette visée, ce sera à vous alors de vous déplacer vers la cible, (l'arbre ici en l'occurrence) pour que les 2 extrémités du bâton vertical viennent coïncider avec les deux extrémités de la chose à mesurer. Etant donné que dès le départ d et h sont choisis égaux eh bien vous aurez forcement D et H qui seront aussi égaux suivant toujours ce théorème de Thalès des égalités d/D = h/H. En mesurant la distance D du pied de l'arbre quand vous obtenez la bonne visée, vous aurez la hauteur H de l'arbre.
Dessin qui illustre cette méthode du bûcheron, en utilisant toujours cette relation de Thalès…
Autre méthode, en sortant votre sextant* de sa boîte feutrée…
Cette fois on va utiliser les fonctions trigonométriques et les rapports dans le triangle rectangle.
Vous faites un relevé de la hauteur en connaissant la distance précise D au pied de votre mât. Cette mesure n'est pas toujours aisée à connaître. Cependant si elle est éloignée, d'abord cela sera mieux mais surtout vous pourrez le faire en vous aidant du Radar. En effet, au Radar vous repérez un endroit précis au sol (obstacle…), sur l'eau (bouée, bateau…) que vous plotez à l'aide des boutons adéquat sur votre écran et vous avez ainsi sa distance avec précision. Vous irez ensuite vous mettre sur cet endroit exact pour effectuer le relevé du haut de votre mât (et antenne) au sextant. Notez l'angle, degrés et minutes de degré.
Ensuite reste à exploiter la règle des triangles rectangles… A savoir, partant d'un angle, le côté opposé du triangle est égal à son côté adjacent X par la tangente* de cet angle. (rappel : la tangente est le rapport de longueur du côté opposé sur le côté adjacent donc H/D).
Le côté opposé (H) sera la hauteur à mesurer.
Le côté adjacent est la base (D), distance au pied du mât
L'angle (α), la mesure relevée au sextant en degrés et minutes.
Deux exemples concrets…
A) Je suis à 40m du pied du bateau, je relève au sextant le haut de l'antenne du mât à 17°30'…
Quelle est la hauteur de l'antenne au dessus du sol (de l'eau !) ?
Soit la formule H = D X tg α
Dans la table il y a 17°30' soit, tg = 0,315
Réponse, le mât à une hauteur totale de…:
H = 40m X 0,315 = 12 ,60 m
B) Vous êtes à 0,225 Nm d'un pont (endroit où vous voulez passer, mesuré au Radar). Votre sextant vous donne une hauteur relevée entre le dessous du tablier et l'eau de 6°20'.
Quel est le tirant d'air sous le pont ?
Soit, toujours la formule H = D X tg α
Convertir 0,225 Nm en mètres, soit 416,70 m
Dans la table on prend au plus proche de 6°20' et on arrondit…
(soit tg 6° = 0,105 puis tg 6°30' = 0,114. On prendra, "à la louche", au plus près et moyenné donc pour tg 6°20' = 0,111).
Réponse, le tirant d'air sous le pont est de… :
H = 416,7 X 0,111 = 46,25 m
*Sextant : Vous allez me dire…mais je n'ai pas de sextant !
Comment faire ?
Qu'à cela ne tienne, nous allons en fabriquer un, plus exactement ce sera un astrolabe comme nos marins d'antan !
* Fonction trigonométrique, tables… : Si vous n'avez pas de Tables Trigo en voici une ici… vous pourrez même la copier sur votre ordi, elle est en format Word, restreinte en 2 pages seulement, mais bien suffisante.
Vous pouvez la télécharger, ici...
Faire un astrolabe…
Il suffit de regarder ce dessin, en faire autant et vous aurez aussitôt votre astrolabe opérationnel pour faire des mesures. Certes, il ne sera pas aussi fiable et précis qu'un sextant mais qu'importe, il permettra de faire des relevés suffisamment probants.
Cela ressemble à un clinomètre de géologue (ou encore inclinomètre) quelque peu ressemblant également à nos "gitomètres" de bateau !
Vous prenez une feuille cartonnée et vous tracez un quart de cercle avec ses portions de fromage. Il faut y faire un trou en haut et y mettre une aiguille qui se balancera en fil à plomb (j'ai pris un bout de fil électrique rigide). Enfin vous collez, avec deux bouts de scotch, une paille sur le bord supérieur qui servira de lunette de visée.
L'astrolabe, votre pseudo sextant est fini !
Fabriquer un astrolabe en reproduisant ce dessin…
Comment faire la visée...…ici, …démo… :
Mesurer la distance d'un amer…
Parfois il peut être intéressant d'avoir une idée précise de la distance d'un amer. Le sextant est tout indiqué pour ce faire si vous connaissez la hauteur en mètres de cet amer (cas d'un phare au-dessus de l'eau, également un point géodésique côté, ou autre…). Vous faites alors un relevé de la hauteur apparente de cet amer, en degrés et minutes d'arc. Maintenant, connaissant sa hauteur réelle en mètres et cet angle apparent, vous pourrez calculez sa distance par la formule suivante…
D = 1,852 X H/ho. ou D sera la distance en milles* nautiques
H = hauteur de l'amer en m, donnée aux documents nautiques.
ho = hauteur observée, traduite en minutes (1° = 60 minutes).
On peut reprendre l'exemple précédent d'ailleurs, ce qui permet de vérifier les formules…
6°20' = 6° X 60' + 20' = 380' (avec hauteur de passage sous le pont de 46,25 m)
D = 1.852 X 46,25 m / 380' = 0,225 Nm (c'était bien la distance mesurée au Radar dans notre exemple).
Incroyable mais vrai, ça tombe juste !
* Le mille chez les nos voisins english fait 1853,18 m. Ils ont toujours voulu faire différent ces « roulent-à-gauche ». Mais bon, nous ne sommes pas à un mètre près ; prenons le nôtre, 1852 pour le calcul (cela rendra hommage à Napoléon III qui devint Empereur des Français cette année-là).
NB : Cette méthode ne peut être employée que pour les distances relativement proches, inférieure à 5 - 6Nm en pratique. En effet si votre amer commence à disparaître, les pieds derrière l'horizon apparent, votre relevé d'élévation sera faussé (plus petit) à cause de la rotondité de la terre. La perte de mesure, au calcul, vous donnera une distance plus éloignée que la réalité.
Mesurer la largeur d'une rivière, d'un canyon, d'un terrain sans accès…
A l'aide de votre boussole !
Non, ne riez pas je ne suis pas encore atteint de sénilité précoce…
Oui, cela peut paraître totalement incongru et pourtant, cette méthode est très facile, sans aucun calcul, vraiment sans rien d'autre qu'une boussole. On va exploiter simplement les rapports de grandeur dans un triangle particulier : le triangle isocèle rectangle (TIR)…
Qu'est-ce-que-ça-que-ça-que-c'est ?
Voici un dessin avec largeur de la rivière à mesurer.
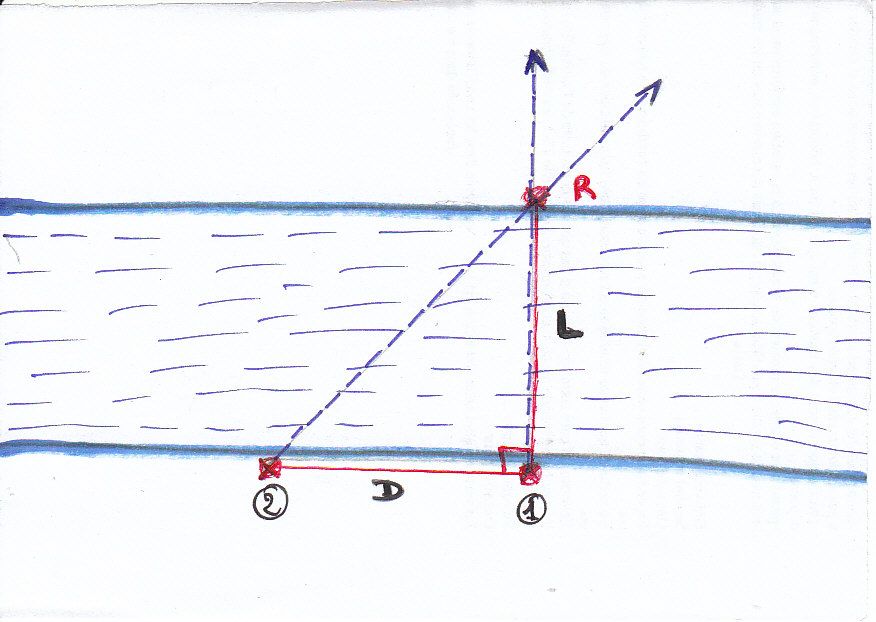
On se positionne au point (1). Ensuite on repère un arbre ou un point remarquable en face, à 90° (à angle droit du bord de la rivière) sur la berge, le point (R) - arbre, rocher, endroit remarquable....
Et là, on vise ce repère pour en connaître la direction géographique sur la boussole – on lit, par exemple 032°. Bien.
Ensuite il faut marquer cet emplacement (1), au sol, où l'on a fait la visée.
Là, deux solutions différentes vont s'offrir à vous suivant que la berge est praticable vers la gauche ou vers la droite (peu importe si c'est l'amont ou l'aval !)…
Supposons que je parte vers la gauche*. Eh bien je m'écarte de mon premier emplacement (1), tout en visant toujours mon repère en face R et en regardant ma boussole jusqu'à trouver sur celle-ci un angle égal à ma première lecture + 45° ! Pour notre exemple pris : 32° + 45° = 77°
Dès l'instant que le cap a augmenté suffisamment pour atteindre cette valeur : 77°, je m'arrête et je marque ce nouvel emplacement au sol (2).
La distance entre (1) et (2), (D) sera exactement égale à la distance (L) soit la largeur de la rivière.
(une grande enjambée faisant environs 1mètre, c'est facile à mesurer).
CQFD.
Vous allez me dire mais comment est-ce certain, à partir d'une boussole ?
Eh bien, on exploite tout simplement les propriétés bien particulières du triangle isocèle rectangle. Triangle que l'on aura dessiné, en se déplaçant, tout en faisant des mesures, jusqu'à la bonne, obtenue d'avance par une simple addition.
Dans le TIR, l'angle au sommet étant à 90°, la somme des 2 autres est aussi égal à 90° or dans un triangle isocèle les côtés sont aussi égaux donc les angles inscrits seront aussi égaux. Ils feront chacun 45°. D'où ce choix de 45° pour l'écart de mesure. Connaissant un angle et un côté, je connaîtrai forcement l'autre angle et l'autre côté !
C'est aussi simple que cela.
Une manière rigolote de « calculer », une distance à partir d'une boussole.
Avec ça, vous allez sûrement épater vos amis, foi d'un chercheur d'absolu !
* gauche : si je pars à gauche on doit ajouter le cap. Si je partais à droite, il faudrait dans ce cas le retrancher. Exemple : 32° - 45° = 360+45-32 = 347° pour la nouvelle visée à la boussole en partant à droite.
Portée théorique d'un émetteur VHF, d'un phare…
Il peut être intéressant parfois d'avoir une idée de cette portée théorique. On peut dire en simplifiant qu'elle se fait en ligne droite avec des pertes par absorption en fonction de la distance…
La formule est :
P = 1,23 √ H1 + 1,23 √ H2
P = portée théorique en milles (Nm)
H1 = hauteur de la source observée, en pieds (ft).
H2 = hauteur de l'observateur, en pieds (ft).
Si vous voulez utiliser H en mètres, il vous faudra prendre la formule…
P = 2,2 √ H1 + 2,2 √ H2 (mais P reste en Nm).
Rappel……. 1Nm = 1,852 km ou 1 km = 0,540 Nm
Et, l'inverse 1 m = 3,28 ft (pieds) ou 1 ft = 0,305 m
Bon tout ça, ce sont des astuces pour navigateurs un tant soit peu cérébraux… mais ce n'est pas bien sorcier au fond et surtout amusant, sommes toutes, non ?
Cela nous donne l'occasion de faire prendre l'air au sextant car "depuis Kek'temps, ben y sort pas souvent", (euh, sous vent) le bougre !
Qu'on se le dise …et bon vent !
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 246 autres membres